The perceptron is a basic mathematical model for solving Binary Classification problems. It consists of 2 components:

1. Weights & Biases

• You can think of these as knobs that you tweak to get the desired result
• They are just numbers
• The difference between both arises in the learning process

2. An Activation Function

It’s quite limited and can’t solve anything that isn’t linearly separable, for example the XOR problem.

Example

Let’s solve a classic problem, determining whether a point lies below or above a line

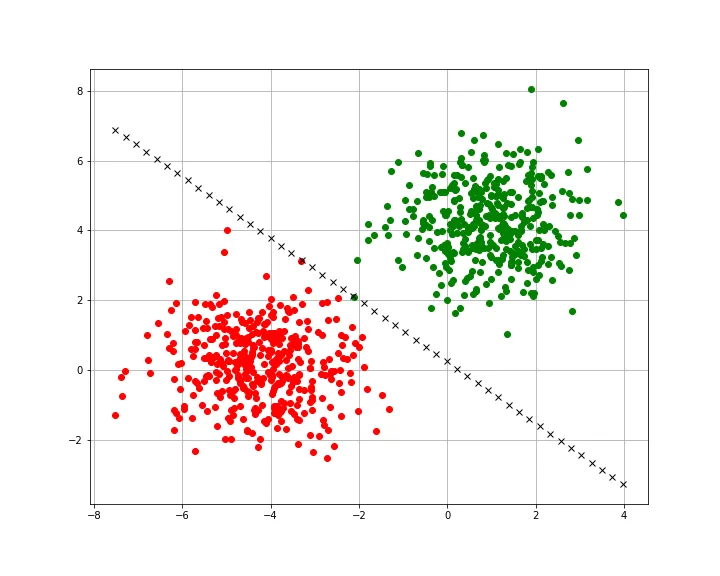
• The input of our perceptron will be the X and Y coordinates of the point.
• The output of our perceptron should be a number, let’s say that $-1$ means that it’s below the line and $1$, above the line.

Prediction

The feed forward (or in other words, the “prediction”) process involves several steps

• Provide some sort of input, $x$ and $y$
• Compute the weighted sum of the respective weights, $w_0x + w_1y$
• Add the bias, $w_0x + w_1y + b$
• Plug the result into an activation function $\operatorname{sgn}(w_0x + w_1y + b)$

$$\operatorname{sgn}(x) = \begin{cases} -1 & \text{if } x < 0, \\ 0 & \text{if } x = 0, \\ 1 & \text{if } x > 0. \end{cases}$$

• The output will determine whether the point lies below or above the line
• The above steps can be summarized as $y = f(\sum_{i=0}^{n}w_ix_i + b)$
• At first, our perceptron will perform very poorly. This is because usually the weights are completely random.

Learning

We can use a simplified version of Supervised Learning to optimize our model.

We can compute the error for our model - $error = y - \hat{y}$. We can then update our weights - $w_i \leftarrow w_i + \alpha \cdot error \cdot x_i$ where $\alpha$ is our Learning Rate and $x$ is our input. We can then also update our bias - $b \leftarrow \alpha \cdot b \cdot error$.

We repeat this process a bunch of times, until our model converges.

An example implementation can be found on my GitHub repo

References

• https://www.wikiwand.com/en/Perceptron