A linear system is a collection of multiple Linear Equations with the same variables. Finding the solution to a linear system involves finding the right variables, such that all equations are satisfied.

Examples

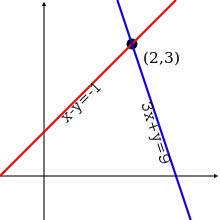
${\displaystyle {\begin{cases}3x+2y-z=1\\2x-2y+4z=-2\\-x+{\frac {1}{2}}y-z=0\end{cases}}}$ With the solution being: ${\displaystyle (x,y,z)=(1,-2,-2)}$

If you plot all of the equations, the solution lies in the intersection of their lines / planes. It could be a single number or an entire set. If there isn’t a common point across all of them – then there are no solutions.

${\displaystyle {\begin{cases}x-y=1\\3x+y=9\end{cases}}}$ With the solution being: ${\displaystyle (x,y)=(2,3)}$

References

• https://www.wikiwand.com/en/System_of_linear_equations